Алгоритм сортування своїми руками

Мета

На мій погляд, зрозуміти, краще ніж запам'ятати. Можливо ця стаття допоможе комусь зрозуміти суть алгоритмів і зекономить час на їх запам'ятовування.

Задача

В цій статті я спробую написати алгоритм-мутант. Cпрощенний, стабільний варіант алоритму швидкого сортування (Stable Quick Sort).

Працювати це має наступним чином:

Розв'язання

Швидке сортування (Quick Sort) - один з найбільш відомих алгоритмів. Цей алгоритм популярний через те, що не потребує додаткової пам'яті, а його складність за O нотацією - n(log n). Цей алгоритм є нестабільним.

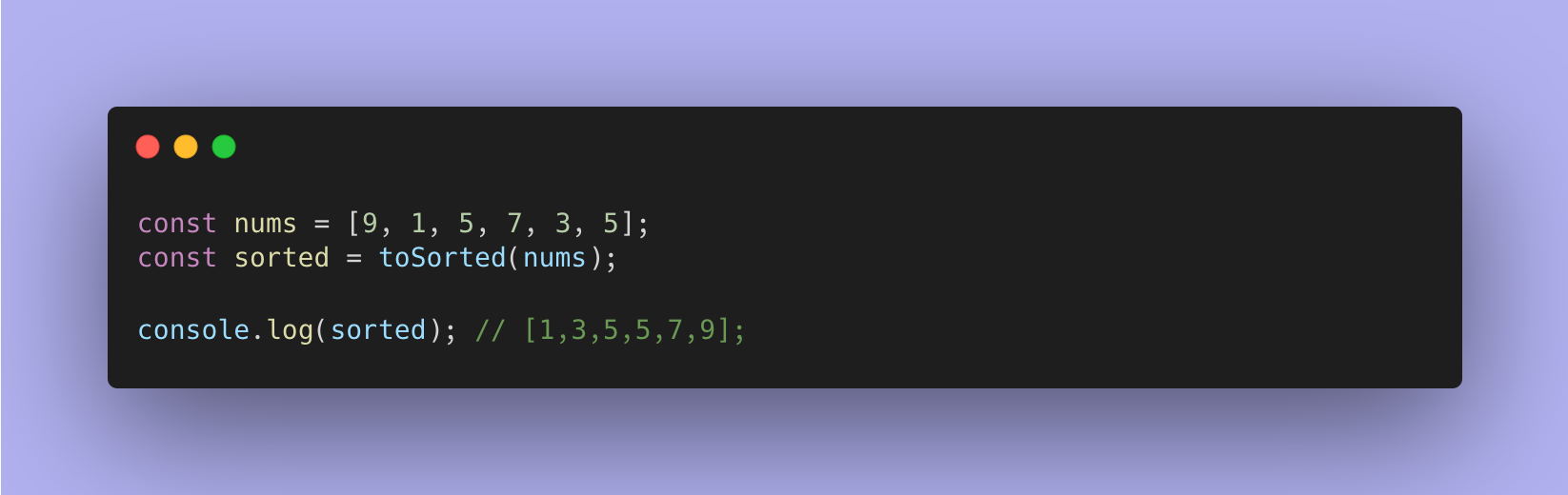
Стабільність алгоритму сортування - властивість яка гарантує збереження порядоку тих елементів, що вже є відсортованними. Приклад:

Мініфікований код для самостійного запуску і експериментів:

                            const products=[{name:"Apple",price:10},{name:"Banana",price:10},{name:"Orange",price:5},],sorted=products.toSorted((e,r)=>e.price-r.price);console.log({products,sorted});
                        

Результат:

Зверніть увагу на позиції Apple і Banana до і після сортування.

Швидке сортування - алгоритм який базується на принціпі "Розділяй і володарюй". Цей алгоритм, як і будь-який інший алгоритм сортування, розглядає поняття "відсортований масив" під своїм кутом.

З точки зору цього алгоритму відсортованний масив - це масив, в якому для будь-якого вибраного елементу справедливі твердження:

• • Всі елементи, що менше вибраного знаходяться зліва від нього


• • Всі елементи, що більше вибраного знаходяться справа від нього


• • Порядок евівалентних виброному елементів не змінюється (наша додаткова вимога до стабільності)

Спробуємо виразити данний список вимог за допомогою JavaScript виразів:

Якщо помістити данний код в тіло функції toSorted, яку ми хочемо написати, то отримаємо наступне:

Для того, щоб заповнити невідомі частини, повернемось до основної чистини визначення:

Відсортованний масив - це масив, в якому для будь-якого вибраного елементу справедливі твердження...

Що це нам дає?

Розглянемо по частинах:

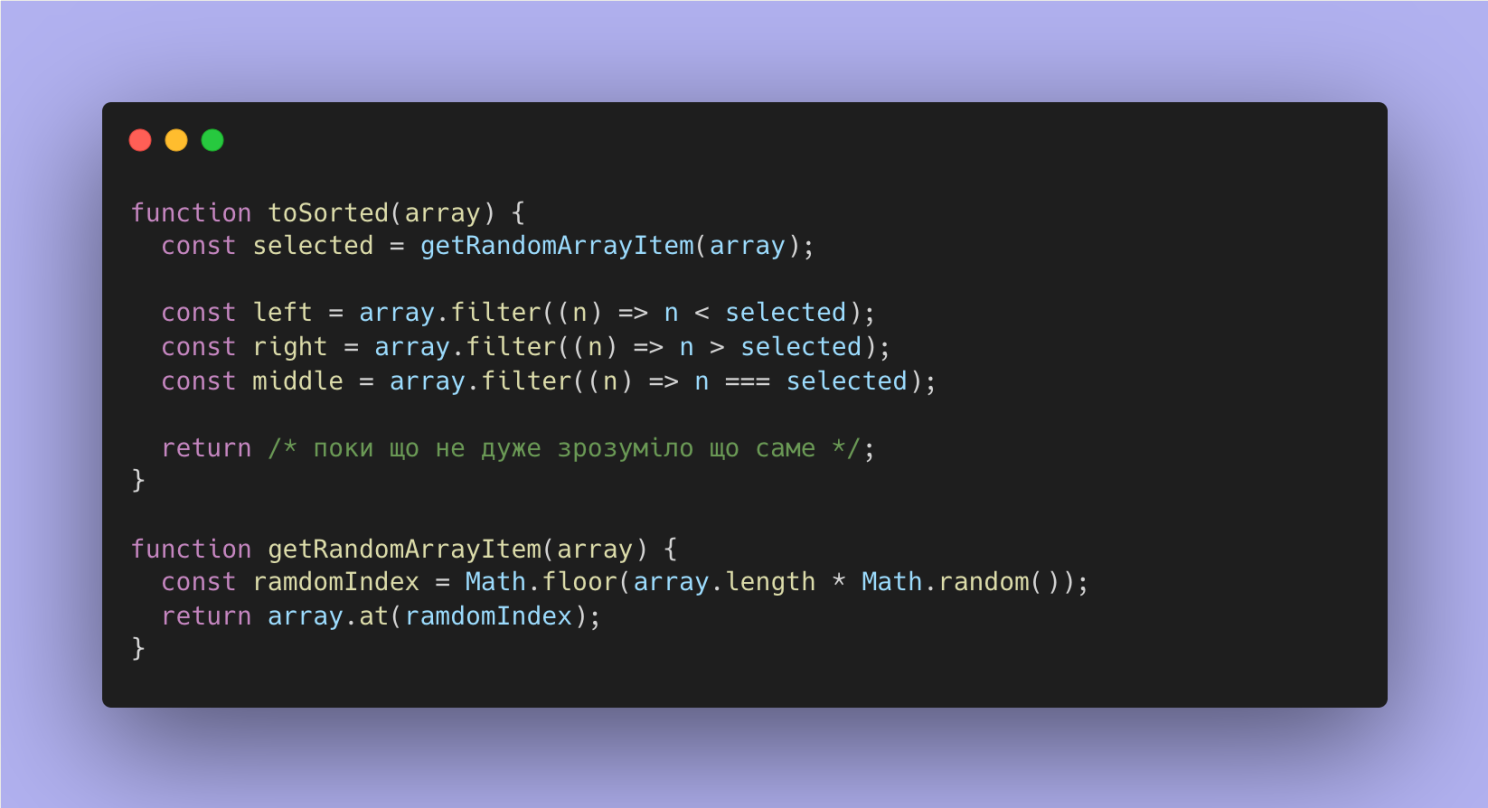
• • будь-якого вибраного елементу - тобто вибраним може бути випадковий елемент. Напишемо окрему функцію яка бере випадковий елемент і додамо до існуючого коду:

  
  
  

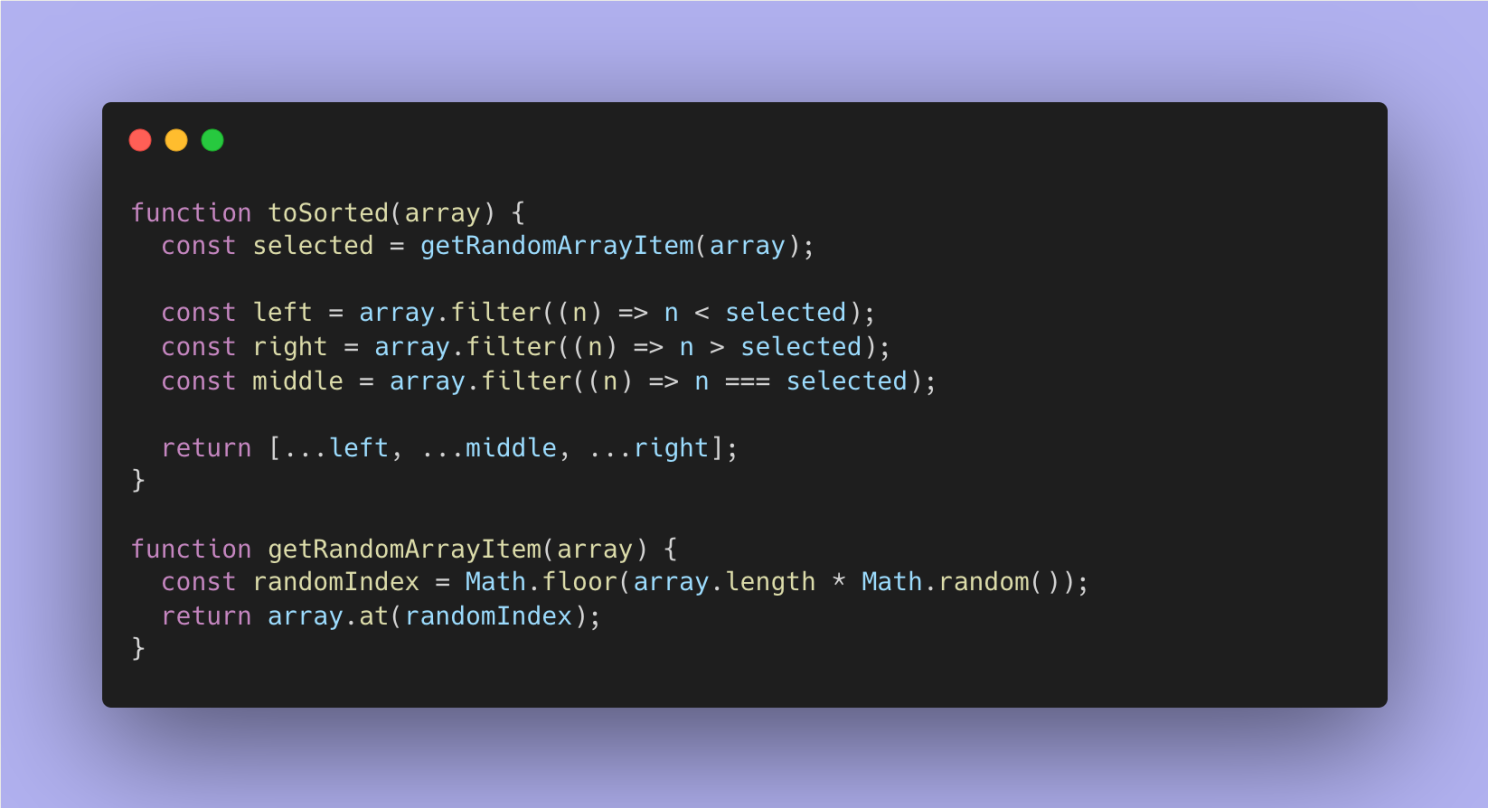
• • Такий масив, в якому ... справедливі твердження - очевидно, що в результаті ми маємо об'єднати все в один масив:

  
  

Таким чином, ми написали код, що відповідає данним вимогам:

Відсортованний масив - це масив, в якому для будь-якого вибраного елементу справедливі твердження:

• • Всі елементи, що менше вибраного знаходяться зліва від нього


• • Всі елементи, що більше вибраного знаходяться справа від нього


• • Порядок евівалентних виброному елементів не змінюється (наша додаткова вимога до стабільності)

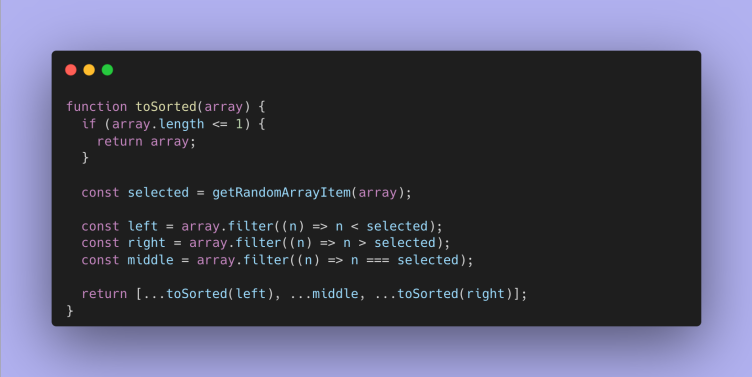
Але зараз ці вимоги працюють тільки для одного, випадкового елементу. Щоб зробити з цього коду працююче рішення, потрібно використати рекурсію.

Рекурсія складається з базового і рекурсивного випадків. У випадку з нашою задачею базовий випадок:

Рекурсивний випадок:

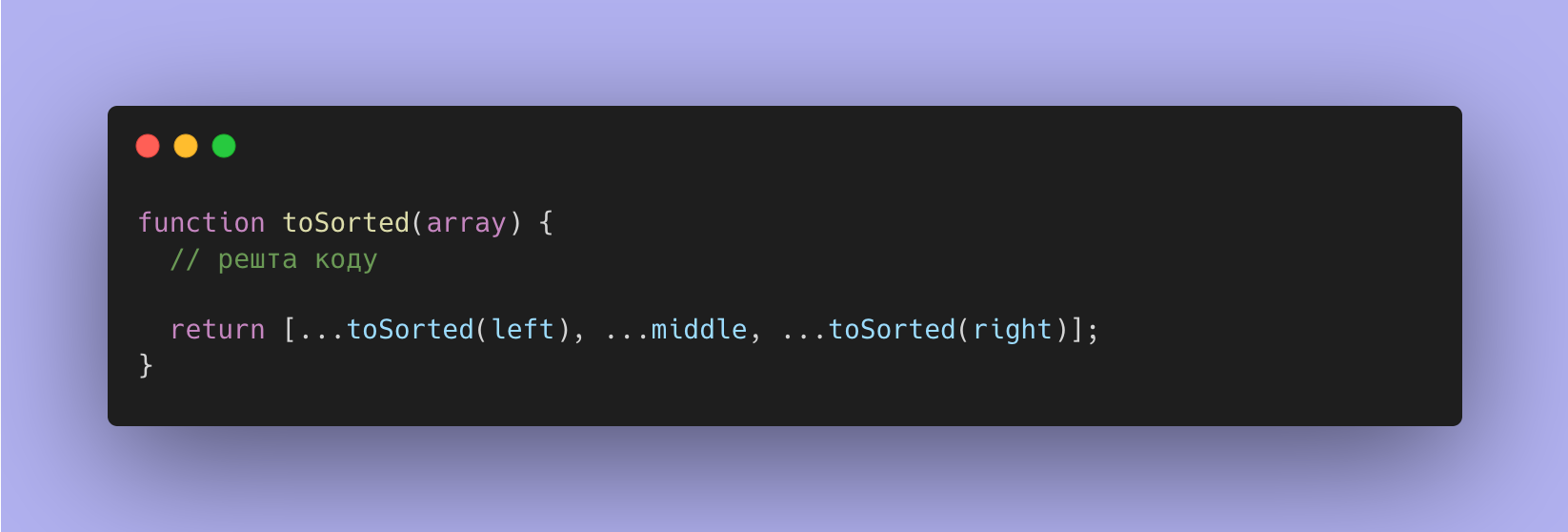
Тож, об'єднаємо весь код разом:

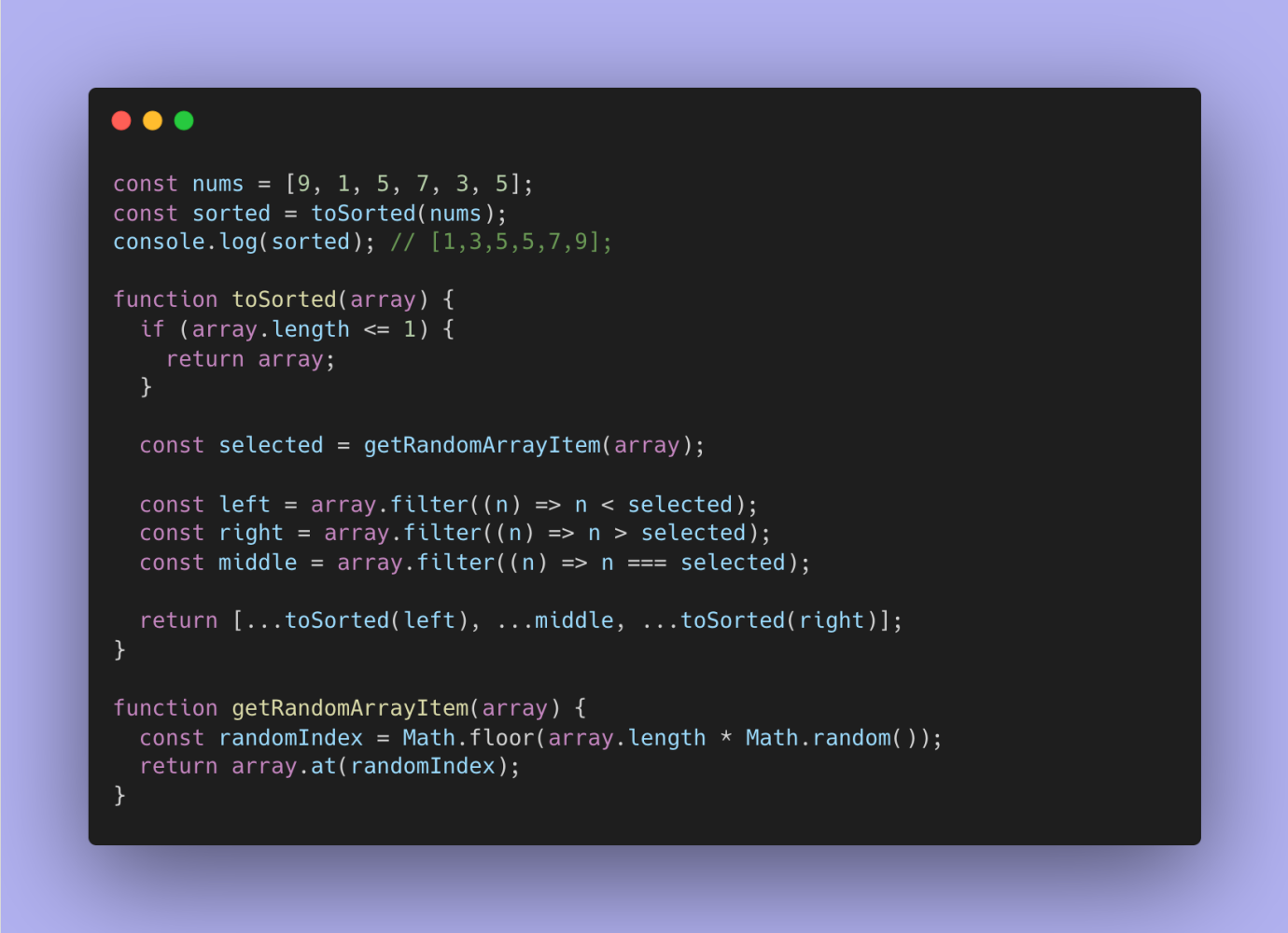
Пробував запускати цей код в консолі Google Chrome. Начебто працює.

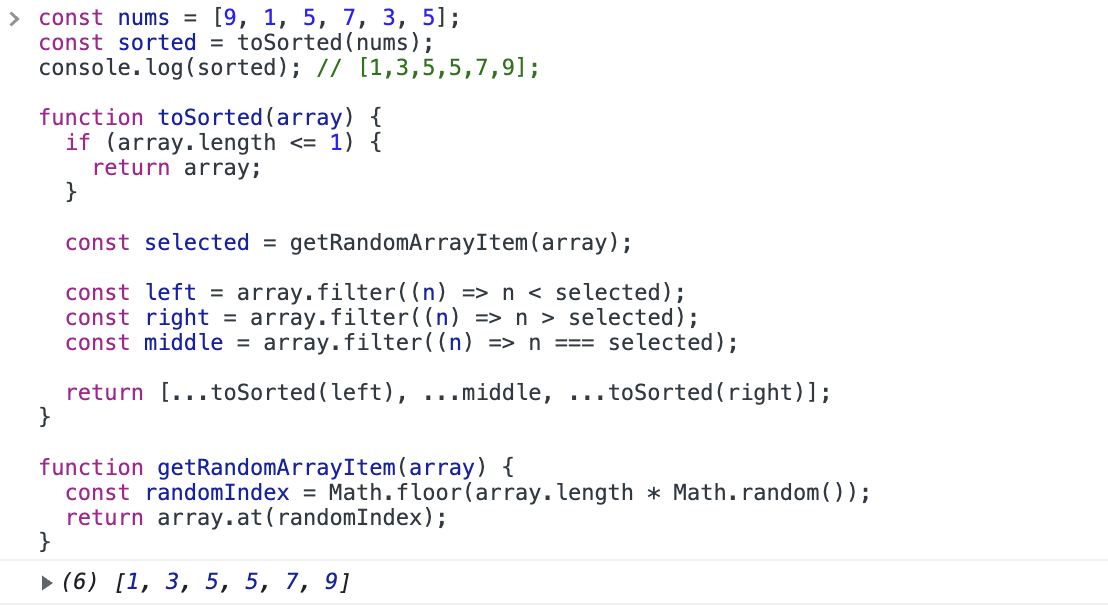
Можете спробувати запустити наступний мініфікований варіант самостійно:

        const nums=[9,1,5,7,3,5],sorted=toSorted(nums);function toSorted(t){if(t.length<=1)return t;let r=getRandomArrayItem(t),e=t.filter(t=>tt>r),n=t.filter(t=>t===r);return[...toSorted(e),...n,...toSorted(o)]}function getRandomArrayItem(t){letr=Math.floor(t.length*Math.random());return t.at(r)}console.log(sorted);
    

Висновок

Отже в данній статті, ми вигадали свої вимоги до алгоритму сортування і написали реалізацію під них на JavaScript. Розв'язання задач таким чином дуже подібне до розв'язання задач з Фізики, Хімії, Математики в школі. Сподіваюсь було цікаво і ви дізнались щось нове.

Джерело: http://surl.li/hawls
Автор: Vladyslav Murashchenko
Адміністратор: Дмитро Берестень